tayawhich.blogg.se - Quadratic inequalities

Look at the following examples, where we apply this process to solve quadratic inequalities. To improve this 'Quadratic inequality Calculator', please fill in questionnaire. We can accomplish this by using the graph or the statements from step 3. The inequality solver will then show you the steps to help you. Solving a quadratic inequality means finding the set of values of the variable, which makes the inequality true. To solve your inequality using the Inequality Calculator, type in your inequality like x+7>9. Step 4: Determine the inequality symbols that will make the solutions found in step 2 satisfy the inequality. If a quadratic inequality is not in one of the four standard forms written above, we must turn it into the standard form, where the most appropriate thing would be to have the coefficient a positive.

Values above the x-axis are greater than 0, and values below the x-axis are less than 0.When the quadratic term is negative, the parabola opens down.When the quadratic term is positive, the parabola opens up and is U-shaped.Step 1: Write the quadratic inequality in standard form. Let us check the definition of quadratic inequality, the standard form, and the examples of quadratic inequalities. the quadratic inequality has been derived from the quadratic equation ax 2 + bx + c 0. And you would learn that the roots of this quadratic function are x is equal to minus 3, and x is equal to 2. The quadratic inequality is a second-degree expression in x and has a greater than (>) or lesser than (<) inequality. So you would say x squared plus x minus 6 is equal to 0. Vary the terms of the inequality and the inequality symbol. Step 3: Obtain a simple graph of the function $latex y=ax^2+bx+c$, or alternatively, consider the following: The test-point method for solving quadratic inequalities works for any quadratic that has a real number solution, whether it factors or not. Because f of x equals 0 when you're intersecting the x-axis. Find the solution set to a quadratic inequality using its graph. We can solve this by factoring the quadratic expression. These types of functions use symbols called inequality.

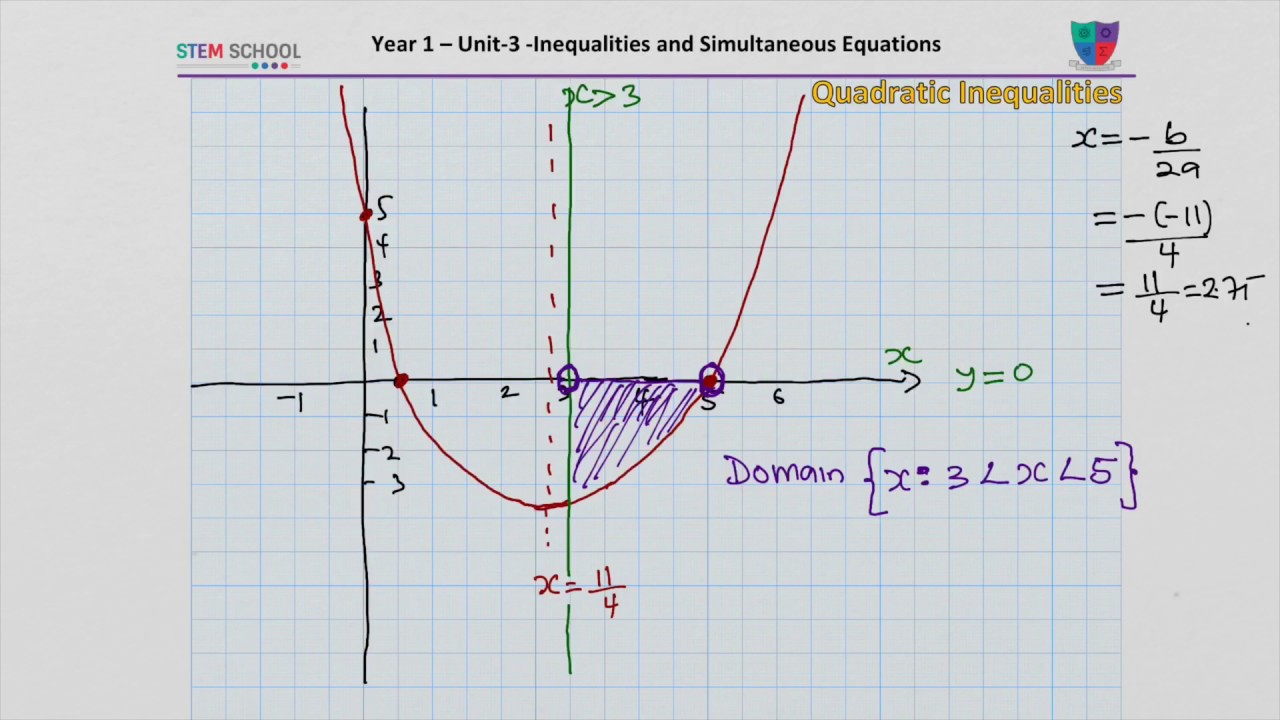
These are the points where the function $latex y=ax^2+bx+c$ intersects the x-axis. A quadratic inequality is a function whose degree is 2 and where the y is not always exactly equal to the function. Step 2: Find the values of x such that $latex ax^2+bx+c=0$. Note: The “>” sign will depend on the problem. Step 1: If it isn’t, write the inequality in the form $latex ax^2+bx+c>0$.

We can solve quadratic inequalities by following these steps: The following are examples of quadratic inequalities: Step 4: Using the graph or otherwise, we need to determine the inequality symbols that will make the solutions found in step 2 satisfy the inequality.Įxplore the examples with answers shown below to understand the application of these steps with real problems.Quadratic inequalities are quadratic expressions that use inequality signs to compare two quantities.

Values below the x-axis are less than 0, and values above the x-axis are greater than 0.

If the quadratic term is negative, the parabola opens down.

If we have a positive quadratic term, the parabola opens up and is U-shaped.

Alternatively, we can solve without a graph by considering the following: Step 3: Sketch a simple graph of the function $latex y=ax^2+bx+c$ to determine the solution. These are the points where the function y a x 2 + b x + c intersects the x -axis. Step 2: Find the values of x such that a x 2 + b x + c 0. Note: The > sign will depend on the problem. To achieve this, we can solve the quadratic equation by factoring $latex ax^2+bx+c=0$ and find the x values. We can solve quadratic inequalities by following these steps: Step 1: If it isn’t, write the inequality in the form a x 2 + b x + c > 0. What happens as you change the value of 'a' By using the check boxes look at what is happening with the regions. Use the Geogebra file to investigate the nature of quadratic inequalities. Step 2: Identify where the graph of $latex y=ax^2+bx+c$ intersects the x-axis. Investigating Regions of Quadratic Inequalities. The “<” sign could be different depending on the problem. Fogel and Chellapilla’s Blondie24 was published over the course of two papers. Step 1: Simplify and write the inequality in the form $latex ax^2+bx+c<0$. To solve quadratic inequalities, we can follow the following steps: 1) Simpify or factorize the inequality which means factorizing the equation in case of quadratic equalities.